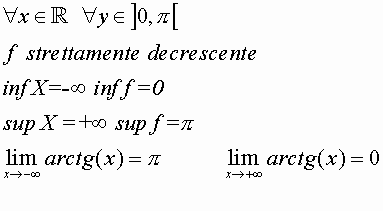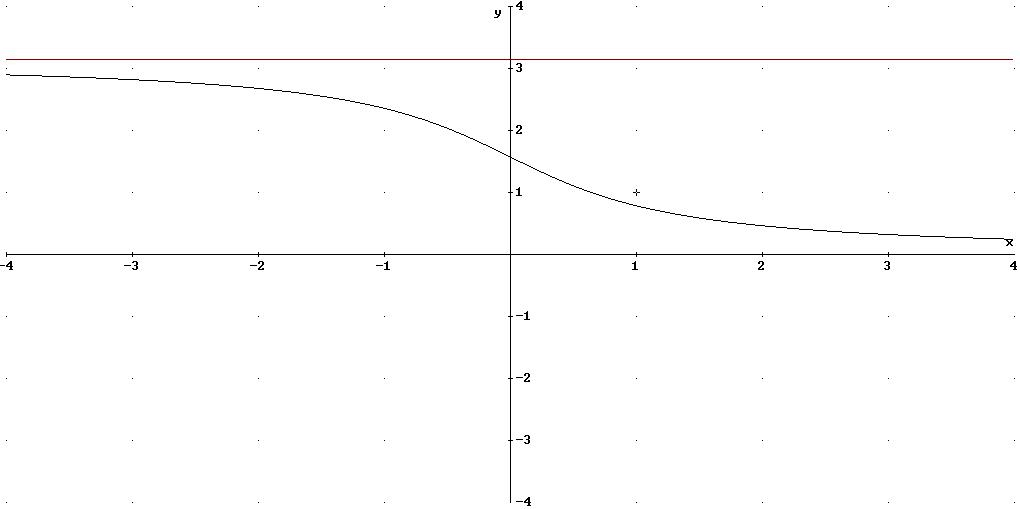Continuità e limite per le funzioni reali di una variabile reale.
Intorni di un punto. Punti di accumulazione
Definizionel. Qualunque sia
, ogni intervallo aperto e
non vuoto di centro
, del tipo
, si
chiama un intorno del punto .
La semidimensione di un intorno si chiama il raggio dell' íntorno.
Indicheremo tale intorno anche sinteticamente con la scritta:
I(xo).
Qualunque sia
l'intervallo
aperto 
si chiama un intorno
di +
e l'intervallo aperto
si chiama un intorno di 
Def.2. Qualunque sia
, per ogni 
l'intervallo
si chiama un semintorno destro del punto
,
I+(xo)
e l'intervallo
si
chiama un semintorno sinistro di xo,
I-(xo)
Oserviamo esplicitamente che qualunque siano i punti distinti x,y, di
esistono un intorno di X e uno di
Y disgiunti.
Def.3. Sia X un sottoinsieme di,
sia 
, appartenente o no ad X. Si
dice che 
è un punto di
accumulazione per X quando in ciascun intorno di
cade almeno un punto di X diverso
da , ovvero, in simboli:
Un punto di X che non sia di accumulazione per X si chiama punto isolato di X.
Ovviamente la proprietà che +¥ , ovvero -¥ , è di accumulazione per X equivale a quella che X è un insieme non limitato superiormente.
Per esprimere che un punto di
accumulazione per X non è ±
¥ , diremo che
è di accumulazione al finito per
X.
E’ facile dimostrare che:
Se è un punto di accumulazione
per X, in ciascun intorno di
cadono infiniti punti di X.
Per un insieme finito non esistono punti di accumulazione. Invece per un insieme infinito esiste sempre almeno un punto di accumulazione. Se l’insieme è illimitato superiormente ( inf.), almeno +¥ (-¥ ) è di accumulazione per X. Se X è limitato, sussiste il TEOREMA DI BOLZANO-WEIESTRASS:
Ogni insieme infinito e limitato ammette almeno un punto di accumulazione.
Def.4 Sia X un sottoinsieme die
sia un punto di
accumulazione per X. Si dice che
è un punto di accumulazione a sinistra per X quando in ciascun semintorno
sinistro di cade almeno un punto
di X diverso da . In modo analogo
si definisce il punto di accumulazione a destra.
Un insieme si dice chiuso quando o non ammette punti di accumulazione(
cioè è vuoto o finito), o ne ammette ma non al finito ( come gli insiemi
) oppure ammette punti di
accumulazione al finito e questi appartengono tutti all’insieme ( come gli
intervalli del tipo [a,b], [a,+¥ [, ]-¥
, b] che sono stati appunto chiamati intervalli chiusi. Diamo allora la seguente
Def.5 Un insieme si dice chiuso quando gli eventuali punti di accumulazione al finito per X appartengono tutti ad X.
Un insieme chiuso e limitato si dice compatto.
Esempi.
l. punti di un intervallo (a,b) con a < b sono tutti di accumulazione per (a,b); anche gli estremi sono di accumulazione per (a,b), e non esistono altri punti siffatti.
-Un intervallo limitato è un insieme chiuso se e solo se gli estremi vi appartengono.
-Un intervallo [a,b] è un insieme compatto; gli intervalli [a, +¥ [,]-¥ , b] sono insiemi chiusi ma non limitati, e quindi non sono compatti.
2. Qualunque punto
è di accumulazione per Q, sicché
esistono punti di accumulazione per Q che non vi appartengono: dunque Q non è un
insieme chiuso. Ovviamente anche R\Q non è chiuso.
3. Ogni punto di un insieme finito X è punto isolato di X. Ogni insieme finito è chiuso, in quanto privo di punti di accumulazione, e quindi essendo anche limitato è compatto.
4. Per l'insieme N non esistono punti di accumulazione al finito; quindi ogni punto di N è punto isolato di N. L’unico punto di accumulazione per N è +¥ -. I:insieme Z ha solo due punti di accumulazione, +¥ e-¥
5. Il punto 0 è di accumulazione per il codominio X della successione( 1/n), dato che per ogni e > 0 all'intervallo ]-d , d [ appartengono infiniti punti del tipo 1/n (basta che sia n > 1/d ). Siccome 0 non appartiene ad X, l'insieme X non è chiuso.
Ovviamente 0 è l'unico punto di accumulazione per X.
2. Le nozioni di continuità e di limite per le funzioni reali di una variabile reale.
Le nozioni di continuità e di limite si riferiscono al comportamento di una funzione "in prossimità" di un punto xo, che deve appartenere all'insieme di definizione se si vuole parlare di continuità, ma non deve necessariamente appartenervi se si vuole parlare di limite, e a tal fine xo, può essere anche ±¥ . Tali nozioni rappresentano diciamo così per evidenziarne l'importanza, il perno su cui ruota l'Analisi Matematica:
Utilizzeremo, ai fini di una maggiore chiarezza, la notazione geometrica, ma va sottolineato che essa non è indispensabile ai fini di una corretta e rigorosa formulazione.
Affrontiamo dapprima il problema della continuità.
Osserviamo le seguenti figure:
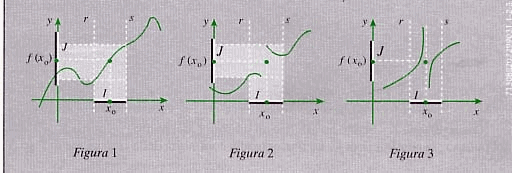
Solo per la figura 1 è valida la seguente:
DEFINIZIONE 1:
Sia f una funzione definita in X e sia
un punto di X.
Si dice che la f è continua nel punto
quando, per ciascun intorno J
di f() esiste un intorno I di
la cui immagine, mediante f, sia
contenuta in J.
In simboli, la continuità di f in
si può esprimere come segue:
In modo analogo si definisce la continuità a sinistra e la continuità a
destra in . Ad esempio:
Sia f una funzione definita in X e sia
un punto di X, di
accumulazione a sinistra per X.
Si dice che f è continua a sinistra nel punto
quando, per ciascun intorno J
di f() esiste un semintorno
sinistro I- di la cui
immagine, mediante f, sia contenuta in J.
In simboli, la continuità di f in
si può esprimere come segue:
Evidentemente:
f continua in 
f continua sia a sinistra che a destra in
DEFINIZIONE 2:
Sia f una funzione definita in X e sia A un sottoinsieme di X
Si dice che f è continua nell’ insieme A quando f è continua in ogni punto
A.
Nel caso A=X si dice semplicemente che f è continua.
LIMITE DI UNA FUNZIONE REALE DI VARIABILE REALE
In generale il comportamento della funzione nei punti di X
appartenenti ad un intorno I di
ma distinti da
non è sempre legato al valore
che la funzione assume nel punto
. Di qui l'importanza di
studiare tale comportamento anche nel caso che
non appartenga ad X, cioè
anche se la funzione non è definita in
(naturalmente, ferma restando
l'ipotesi che sia di
accumulazione per X).
Queste considerazioni conducono in modo naturale al concetto di limite, di cui ora ci occuperemo.
Convergenza
Sia dunque ancora f una funzione reale definita in un
insieme X, e sia un punto
di accumulazione per X, al finito o all'infinito.
Si dice che la funzione f è convergente in
, se esiste un numero reale l
avente la seguente proprietà:
A) Ad ogni intorno J di 1 è possibile associare un intorno I
di in modo che i
valori assunti da f nei punti di I (più precisamente, di x
I), diversi da
, appartengano a J, cioè in
modo che:
(1)
In altri termini la proprietà A) si può esprimere come segue:
qualunque sia l'intorno J di 1, i valori assunti da f intorno
ad 
appartengono
definitivamente a J.
Il numero l si chiama il limite della funzione
f in
.Si dice allora che
la funzione f tende (o converge) ad l in
oppure che f(x)tende ad l
al tendere di x ad o per x
tendente ad e si scrive:
(2)
oppure:
per x
(3)
La scrittura precedente in simboli si esprime pertanto così:
(4)
La denominazione di limite attribuita ad l, e le notazioni (2), (3) sono giustificate dal fatto che, se esiste un numero l avente la proprietà A), esso è univocamente determinato. In altri termini sussiste il teorema
(di unicità del limite):
Una funzione f che sia convergente in un punto
non può tendere ivi a due limiti
distinti
E’ evidente che il discorso sin qui fatto sulla convergenza si può estendere al caso in cui l=+¥ ovvero l=-¥ .
Diremo in generale che:
Se esiste il limite di f in ,
la funzione f si dice regolare nel punto
. Se il limite l è un numero
reale, si dice che in la funzione
è convergente o dotata di limite finito; se l=+¥
si dice che in la funzione è
divergente positivamente; se l=-¥ si dice
che in la funzione è divergente
negativamente. Infine se l=0 si dice che in
la funzione f è infinitesima.
ULTERIORI FORMULAZIONI DELLA DEFINIZIONE DI LIMITE
Osservando la (4) è legittimo porsi il problema di esplicitare con opportune
disequazioni i due intorni I e J di
e di l.
Ad esempio se
ed l è finito, è
possibile esplicitare l’intorno di
mediante un opportuno d e l’intorno di l
mediante un opportuno e , che rappresentano
rispettivamente le semidimensioni. Allora la ( 4) diventa:
(5)
Interpretazione geometrica
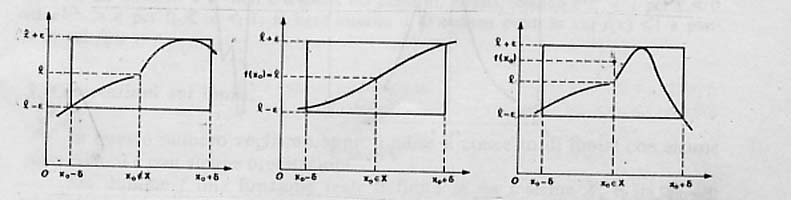
Se la funzione f converge al limite l nel punto xo e se x0 è al finito, ad ogni numero e >0 si può associare un numero d >0 in modo che i punti del diagramma che hanno ascissa compresa tra x0-d e x0+d sono interne al rettangolo di centro P
( xo, l), di lati paralleli agli assi, di base 2d
e altezza 2e . Nelle figure che seguono sono
illustrati sia il caso in cui x0 non appartenga a X nonché il caso
che x0 appartenga ad X, con l= f(xo) e con l¹
f(x0). Naturalmente il punto P appartiene al diagramma solo se
GENERALIZZAZIONE
Possiamo generalizzare la notazione con le disequazioni in tutti i casi, scegliendo di utilizzare sempre e e d , anche se xo ovvero l tendono a ¥ .
Ecco lo schema che si ottiene:
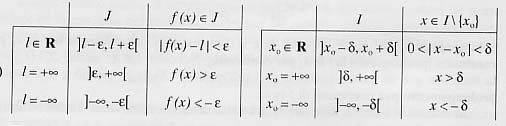
Ad esempio, nel caso in cui
e, nel caso in cui
Lasciamo al discente la formulazione degli altri casi.
Qualche volta può essere utile, per evidenziare maggiormente che il valore di d dipende dal prefissato numero e , scrivere d e al posto di d . Noi non ne ravvisiamo la necessità.
Se la funzione è una successione, diciamola
basta tener conto che per
l’insieme
l’unico punto di
accumulazione è +¥ , perciò l’uguaglianza:
si esprime come segue:
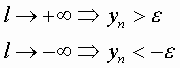
LIMITI E CONTINUITA’
Considerazioni analoghe a quelle esposte per la nozione di limite possono farsi per la nozione di continuità: peraltro i vari casi precedenti si riducono ad uno solo, perché x0, non necessariamente punto di accumulazione per X, deve appartenere ad X e quindi non può essere +¥ o -¥ e d’altra parte f(x0) che subentra ad l deve essere un numero reale.
Per esprimere che f è continua in x0 scriveremo:
e questa si può formulare come segue:
(6)
Osserviamo che la (6) non equivale alla (5) con l=f(x0),
perché nella (5) figura la condizione :
,
ovvero 
. La (5) con l=f(x0)
significa:
(7)
e questa equivale alla continuità in x0 solo se x0 è di accumulazione per X. Se infatti x0 è punto isolato, f è evidentemente continua in x0, ma non si può utilizzare la (7), legata al concetto di x0 punto di accumulazione.
LIMITE DELLA RESTRIZIONE. LIMITE SINISTRO E LIMITE DESTRO
Sia A un sottoinsieme dell’ insieme X. Detta g la restrizione di f ad A l’esistenza del limite di x0 in f implica quella del limite in g, ma non viceversa;cioè può accadere che esiste il limite di g ma non il limite di f.
Si osservino ad esempio i seguenti diagrammi:
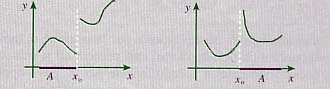
Entrambe le funzioni non sono regolari in x0. Ciò nonostante la restrizione all’insieme indicato con A è regolare ( nel primo caso convergente, nel secondo divergente positivamente).
Diamo alcune definizioni:
Sia f una funzione definita in X e siano A un sottoinsieme di X, x0 un punto di accumulazione per A. Se la restrizione di f è regolare in x0, il suo limite si chiama limite di f sull’ insieme A e si denota con il simbolo:
(*)
Nel caso particolare:
il punto xo è di accumulazione a sinistra (ovvero a destra ) per X e il limite si chiama limite sinistro (destro) di f in xo: In luogo della (*) si adopera allora una delle notazioni:
che, nel caso in cui il punto xo è finito, si traducono ad esempio nelle seguenti definizioni:
Quando xo è di accumulazione sia a sinistra che a destra, la proposizione:
f è regolare in xo ed ha ivi per limite l
equivale alla seguente:
f è regolare in xo sia a sinistra che a destra e
Di conseguenza, se i limiti sinistro e destro di f in x0 esistono entrambi e sono distinti, la funzione f non è regolare in xo.
Esempi
Le funzioni seno, coseno, tangente e cotangente non sono regolari in
Detta f una di tale funzioni, ragioniamo per assurdo e ammettiamo che
esista il limite di f in +¥ , diciamolo l.
Allora, scelto un intorno J di l che non contenga il condominio di f,
sicché risulta: [-1,1]
J,
deve esistere un intorno I di +¥ , tale
che: 
e ciò è impossibile, perché
essendo f periodica risulta
.
Data la funzione: 
,
risulta:
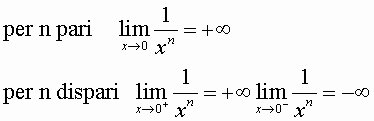
pertanto per n pari è regolare, per n dispari non è regolare.
la funzione: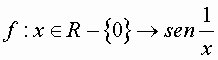 
non è
regolare in 0 anche a destra e a sinistra.
TEOREMI FONDAMENTALI PER LA RICERCA DI UN LIMITE
Siano f e g due funzioni definite in X, regolari in un
punto 
, di accumulazione per
X. Se risulta:
(1)
si ha: 
intorno ad (2)
sicché intorno ad il
diagramma di f è situato al di sopra del diagramma di g.
Viceversa, però, dalla (2) non si può desumere la (1). Se infatti vale la (2) come ipotesi, ne segue che:
Dal teorema precedente, se g(x) è costante, segue:
Se f è una funzione regolare in un punto
, per
vale l’implicazione:
intorno ad
In particolare, per 
si
ottiene il teorema della permanenza del segno:
Ogni funzione regolare in un punto
avente limite
positivo[negativo] in è
positiva[negativa] intorno ad .
Quale è la relazione tra i limiti di successione e i limiti di funzione?
Osserviamo preliminarmente il seguente teorema:
Se è punto di accumulazione
per l’insieme X , esiste una successione di punti di
che tende ad
Da esso segue il teorema che indica la relazione richiesta:
Condizione necessaria e sufficiente affinché la funzione f, definita
nell’insieme X, sia regolare in un punto
di accumulazione per X è che,
per ogni successione di punti 
di
punti di tendente ad
, esista il limite della
successione :
…
Tale limite è allora indipendente dalla particolare successione
e coincide con il limite di f
in
CRITERIO DI REGOLARITA’ PER IL CONFRONTO
Siano f una funzione definita in X e sia
un punto di accumulazione per
X. Se esistono due funzioni 
convergenti in allo stesso
limite, e se risulta:
intorno ad
allora anche f è convergente in
ed ha ivi per limite l.
Il teorema, per ovvi motivi, è detto anche teorema dei carabinieri.
Nel caso della divergenza, il teorema precedente assume questa forma:
Siano f una funzione definita in X e sia
un punto di accumulazione
per X. Se esiste una funzione f divergente positivamente in
, tale da risultare:
intorno ad
allora anche f diverge positivamente in
.
Ad esempio, dalla disequazione
Il seguente teorema è detto anche "criterio di convergenza a 0"
Siano f e g due funzioni definite in X e sia
un punto di accumulazione per
X.
Se f è infinitesima in ,
ovvero:
e g è limitata
intorno ad ( ovvero se
esiste un intorno I di tale
che f è limitata in 
, il che
equivale a dire che esiste un K>0 tale che
)
allora: 
Si osservi che una funzione limitata intorno ad
può anche non essere regolare
nel punto . Ad esempio la
funzione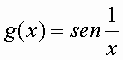
è limitata intorno a
0 ma non è regolare in 0.
LIMITI DELLE FUNZIONI MONOTONE
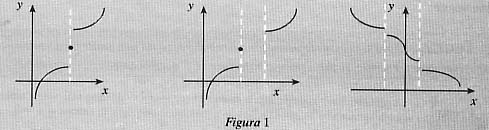
Osserviamo i diagrammi delle figure qui sotto. Scelto comunque un punto
di accumulazione a sinistra o a
destra per l’insieme di definizione di una delle funzioni, sulla base
dell’interpretazione geometrica del concetto di limite è intuitivo che la
funzione è dotata in di limite
sinistro, ovvero destro.
Orbene questa è una proprietà delle funzioni monotone, come risulta dal teorema che segue; dalla tesi emerge che il limite sinistro [destro] è l’estremo superiore o l’estremo inferiore di una parte del condominio della funzione; anche questo, nei casi della figura, si può constatare geometricamente.
Teorema :
Se è punto di accumulazione a
sinistra , ovvero a destra, per un insieme X, ogni funzione monotona F definita
in X è regolare a sinistra [ a destra] in
. Posto:
se f è crescente, risulta:
mentre, se f è decrescente:
Se, nel teorema precedente, la funzione è una successione, cioè se
l’unico punto di accumulazione
per X è +¥ = sup X e per
=+¥
risulta 
. Pertanto nel caso di
una successione il teorema si può enunciare come segue:
Ogni successione monotona è regolare ed ha per limite il suo estremo superiore se è crescente, il suo estremo inferiore se è decrescente.
Il teorema sulle funzioni monotone trova innumerevoli applicazioni nel caso delle funzioni elementari, applicato al dominio di tali funzioni o ad opportune restrizioni
Diamo alcuni esempi:
LA FUNZIONE LINEARE
Y= aX
LA FUNZIONE POLINOMIO DI PRIMO GRADO
Y = aX+b
a>0 f strettamente crescente
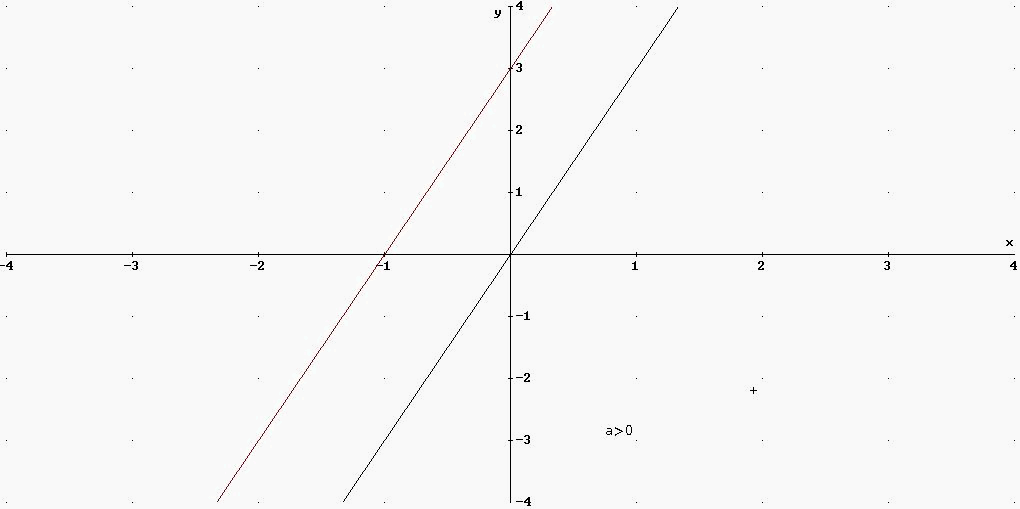
inf X=-¥ inf f= -¥ supX=+¥ sup f=+¥
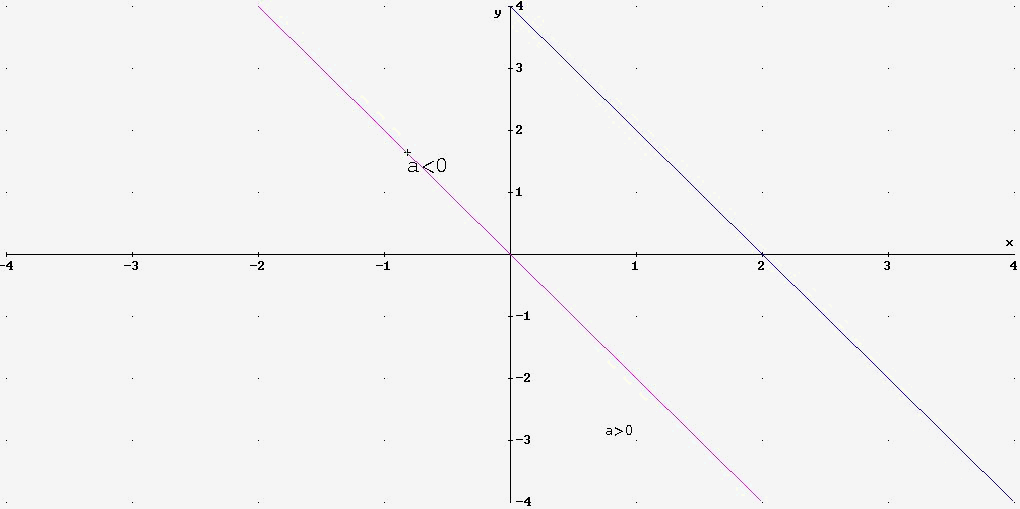
a<0 f strettamente decrescente
inf X= -¥ inf f= +¥ supX=+¥ sup f= -¥
LA FUNZIONE POTENZA AD ESPONENTE INTERO NON NEGATIVO
n intero pari
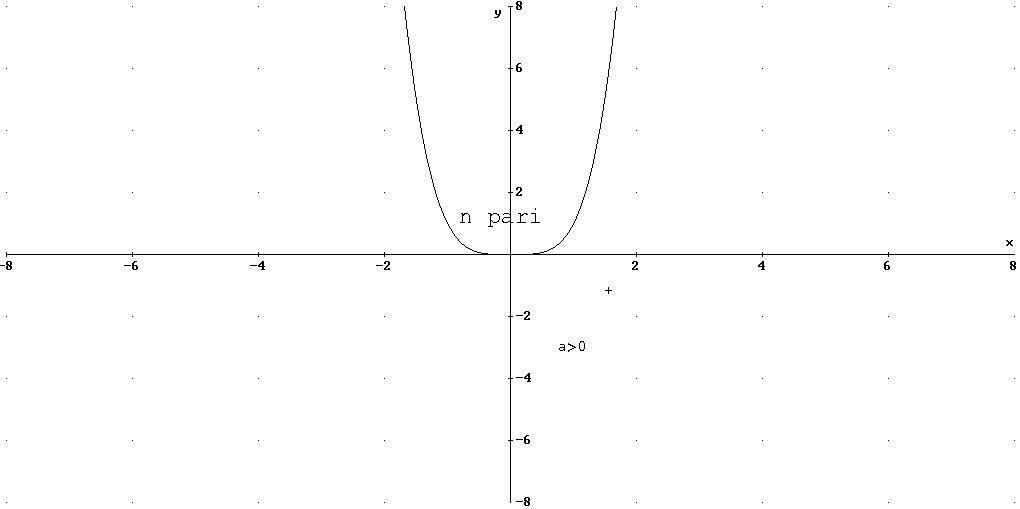
f strettamente crescente in
f strettamente decrescente in
n intero positivo dispari
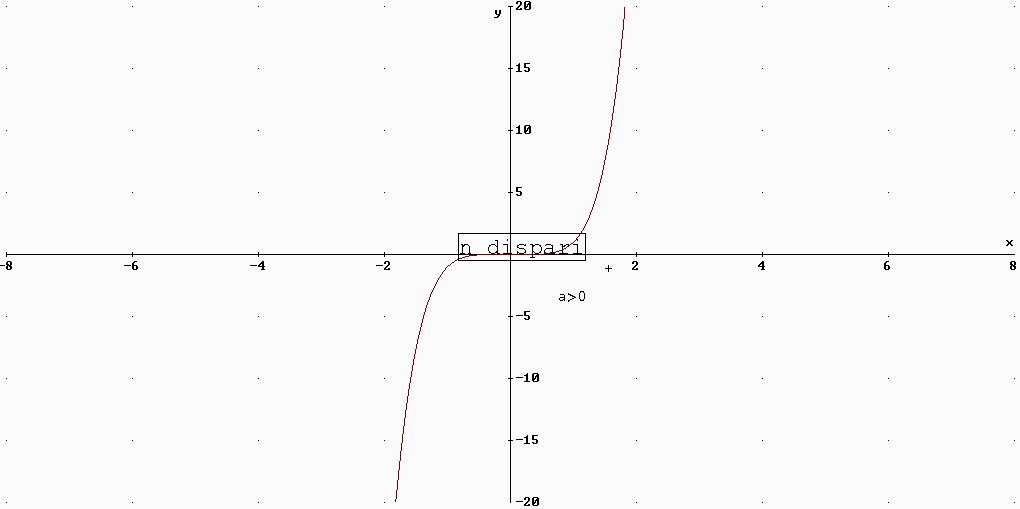
f strettamente crescente in ]-¥ ,+¥ [
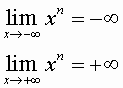
4)LA FUNZIONE POTENZA AD ESPONENTE INTERO NEGATIVO
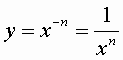
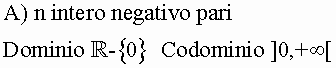
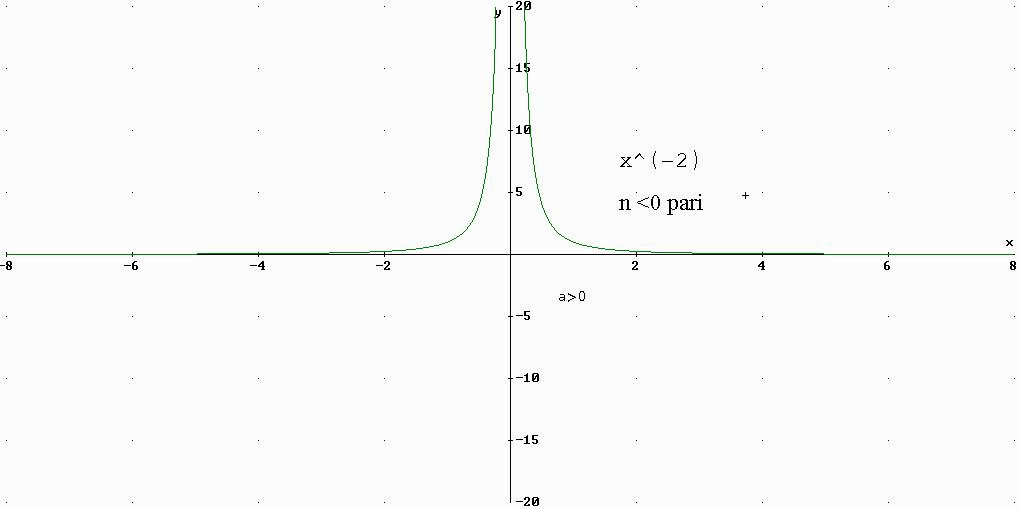
f strettamente crescente in ]-¥ ,0[ f strettamente decrescente in ]0,+¥ [
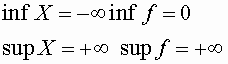
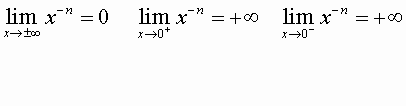
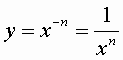
n intero negativo dispari
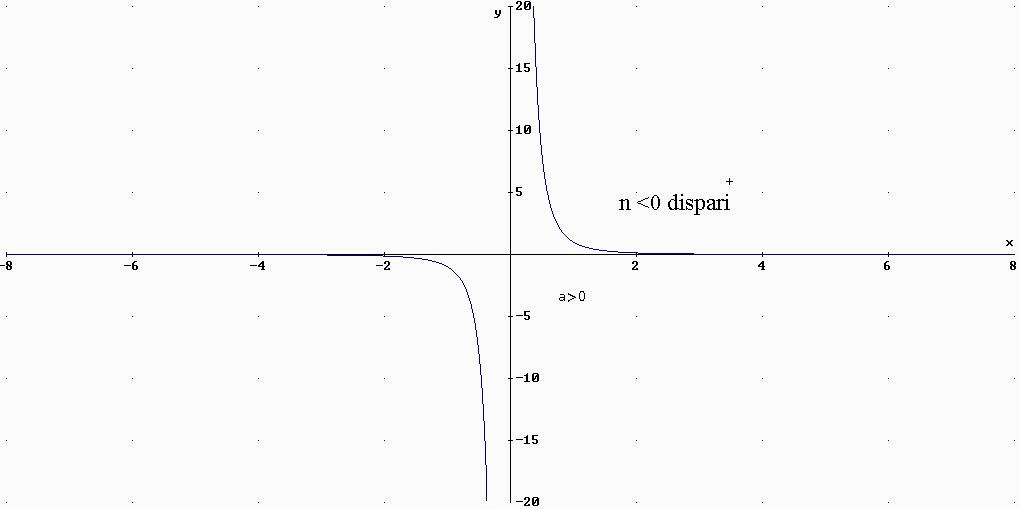
f strettamente decrescente in ]-¥
,0[
]0,+¥
[
5)LA FUNZIONE POTENZA AD ESPONENTE REALE >0
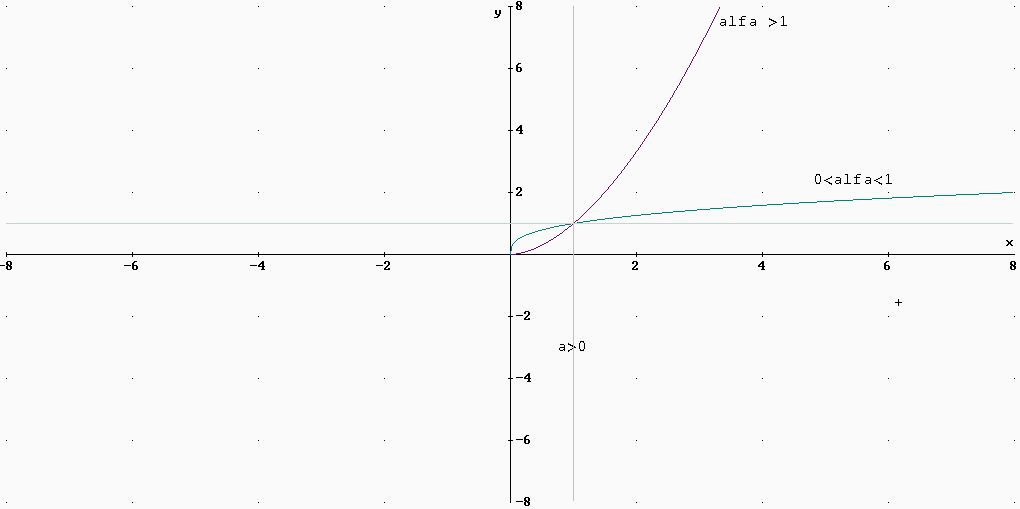
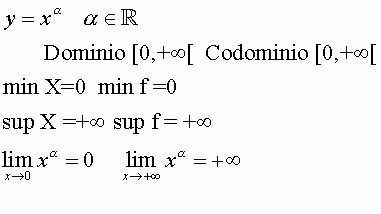
6) LA FUNZIONE POTENZA AD ESPONENTE REALE <0
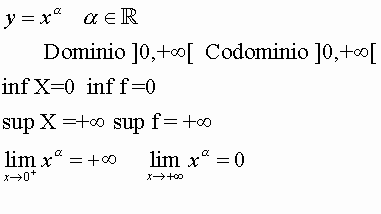
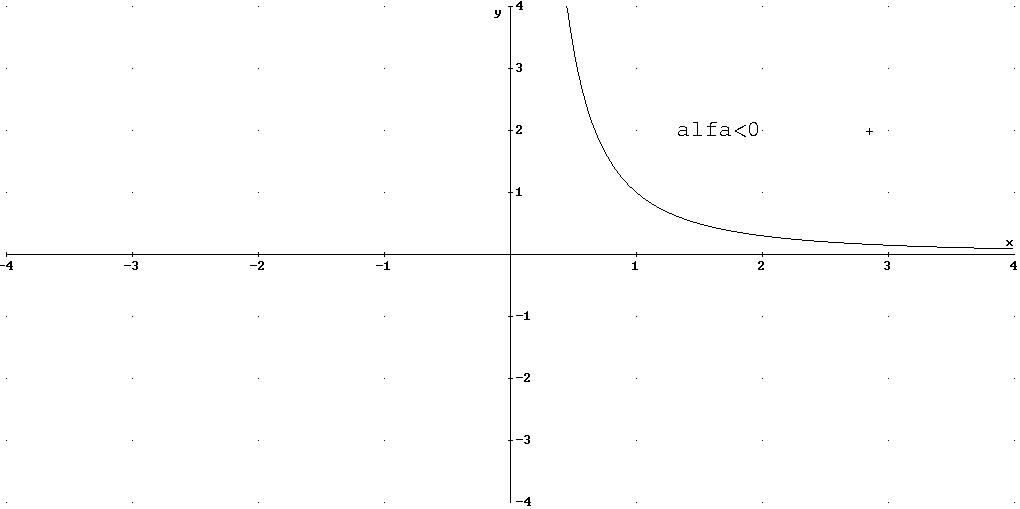
7)LA FUNZIONE RADICE
n pari es:
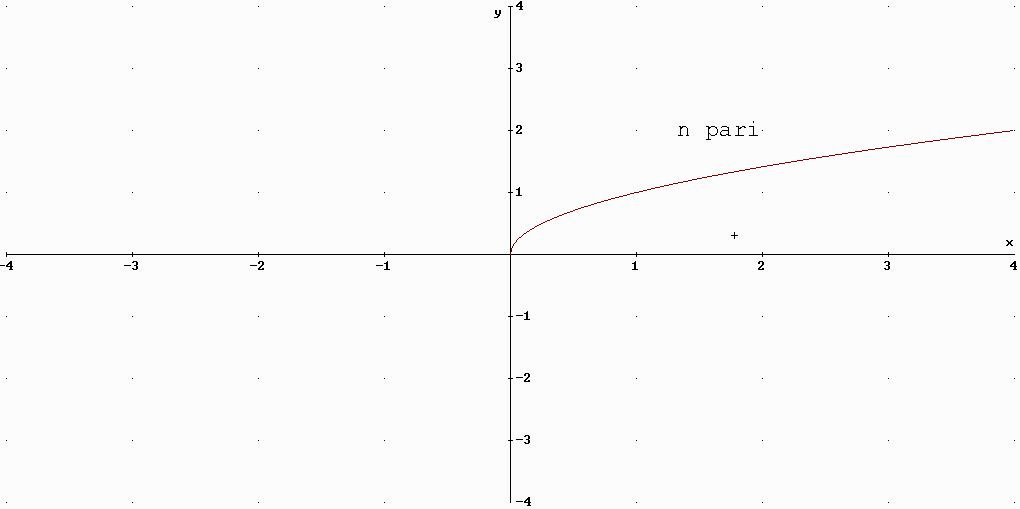
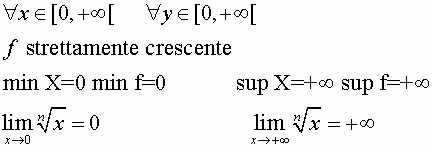
n dispari es: 
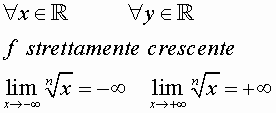
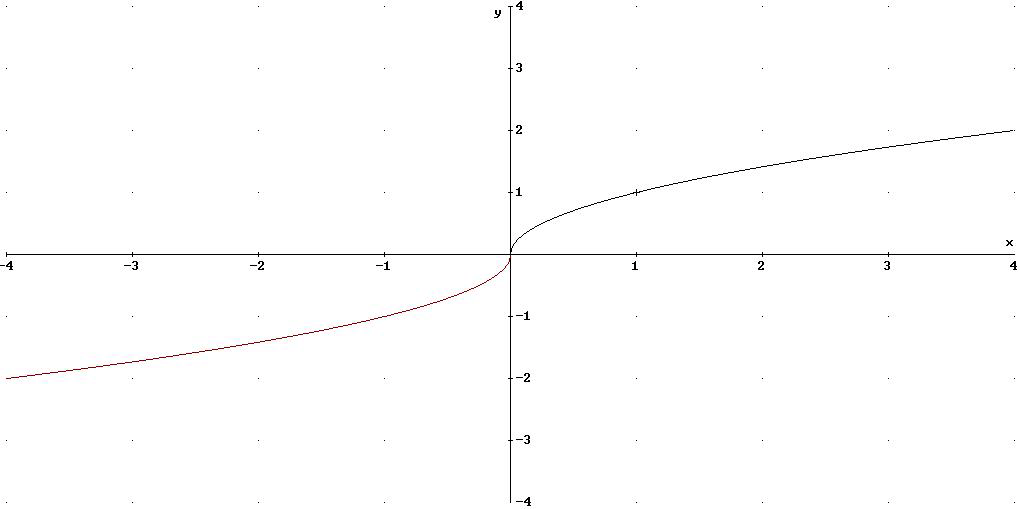
8)LA FUNZIONE ESPONENZIALE
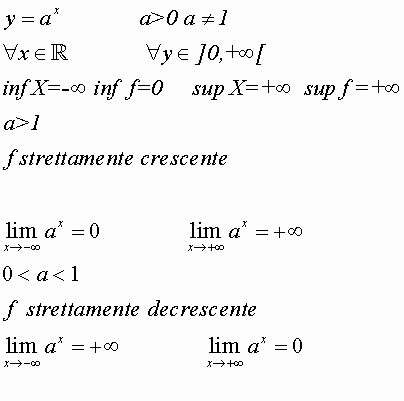
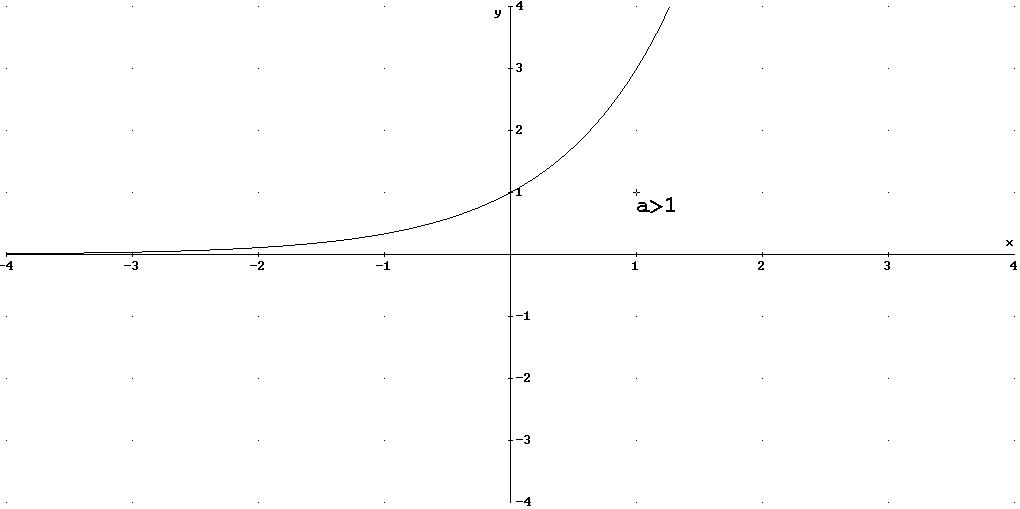
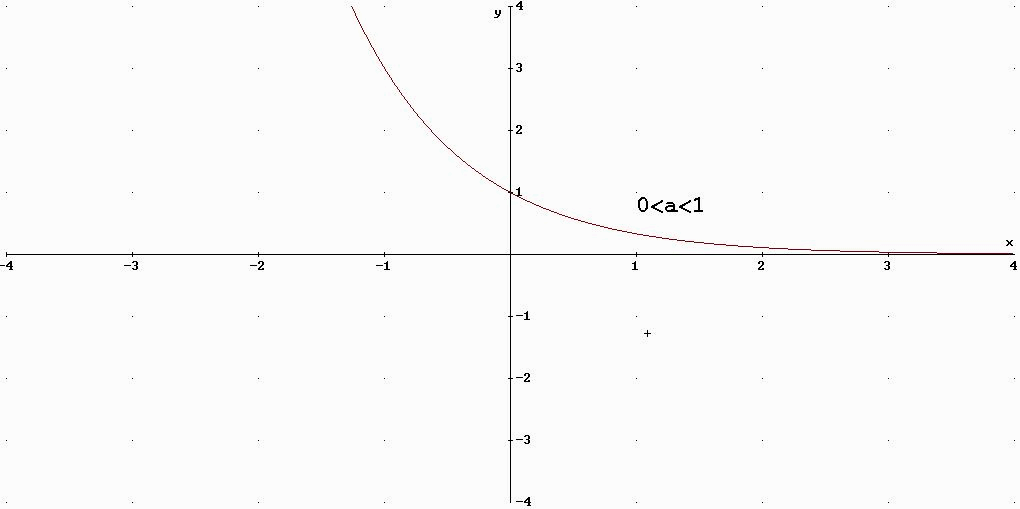
9)LA FUNZIONE LOGARITMO
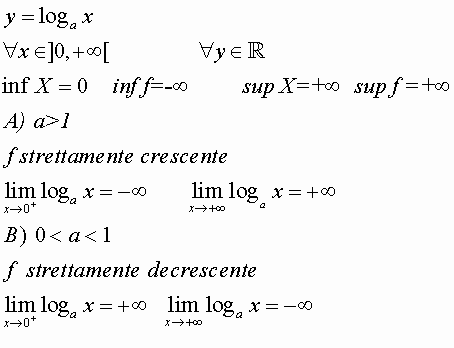
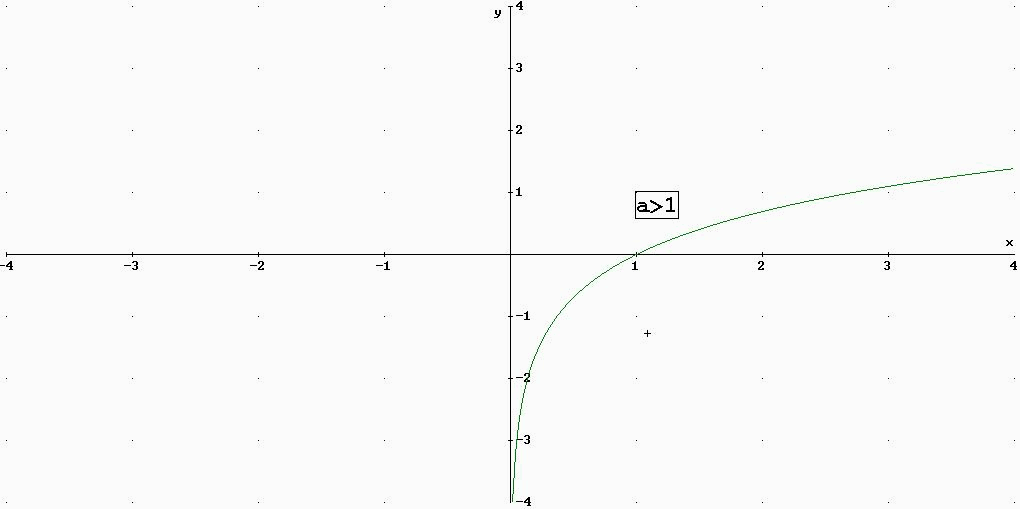
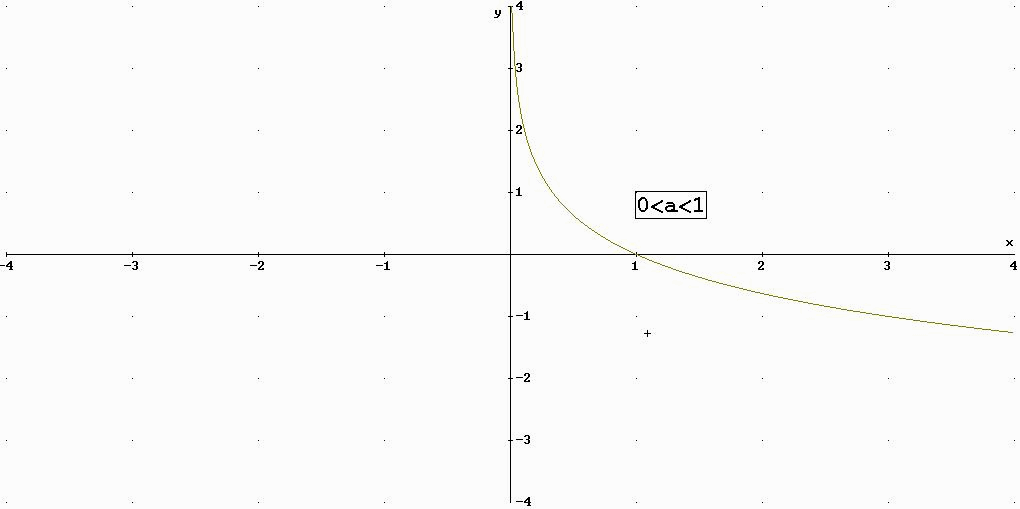
10)LE FUNZIONI CIRCOLARI
Y= sen(x)
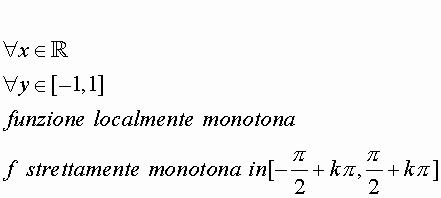
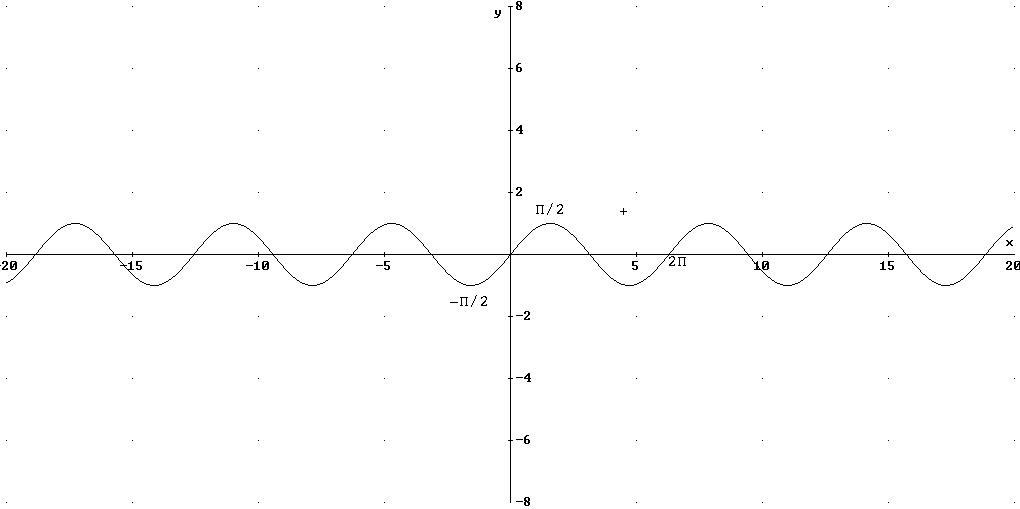
Y=cos(x)
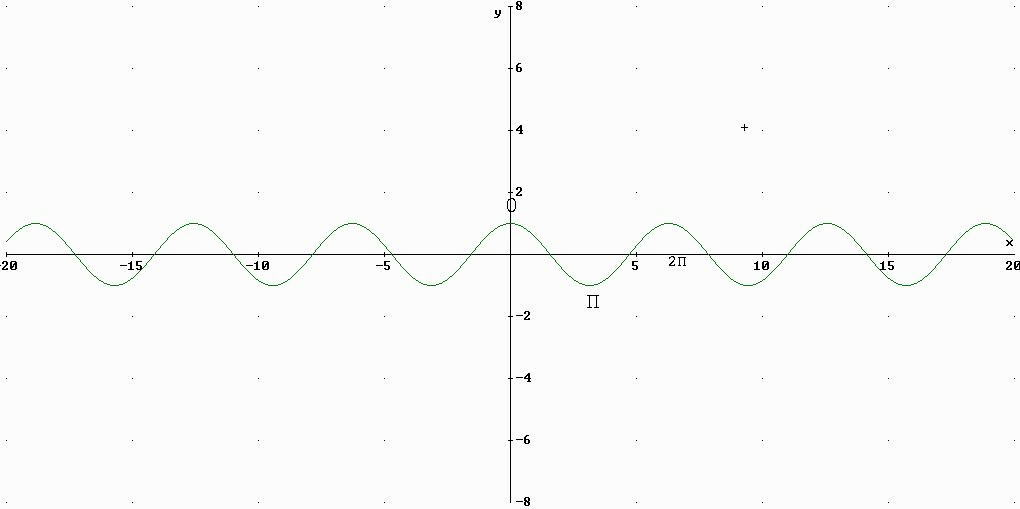
y=tg (x)
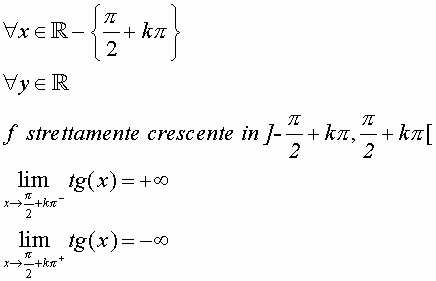
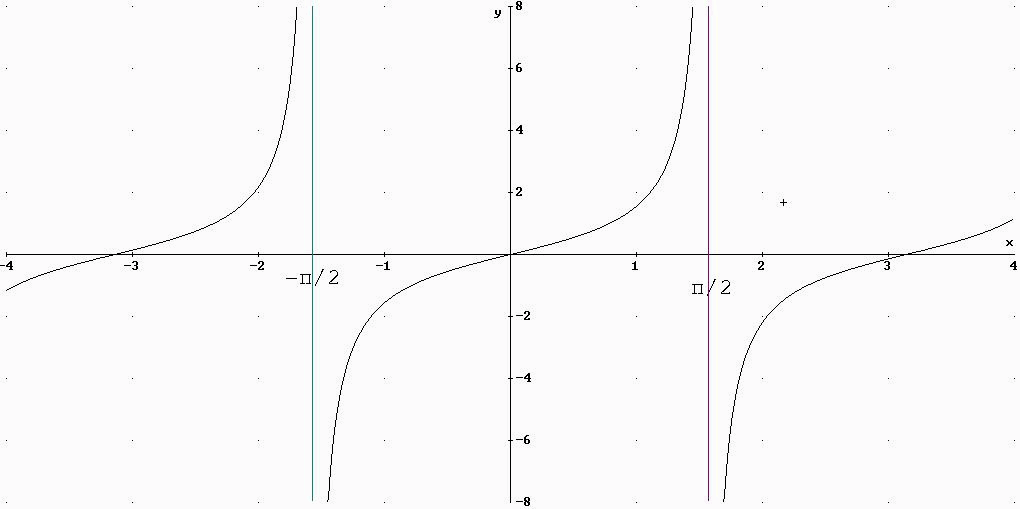
y=cotg(x)
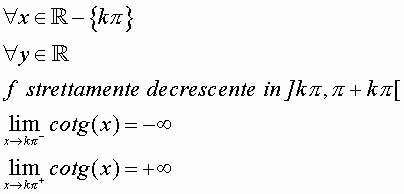
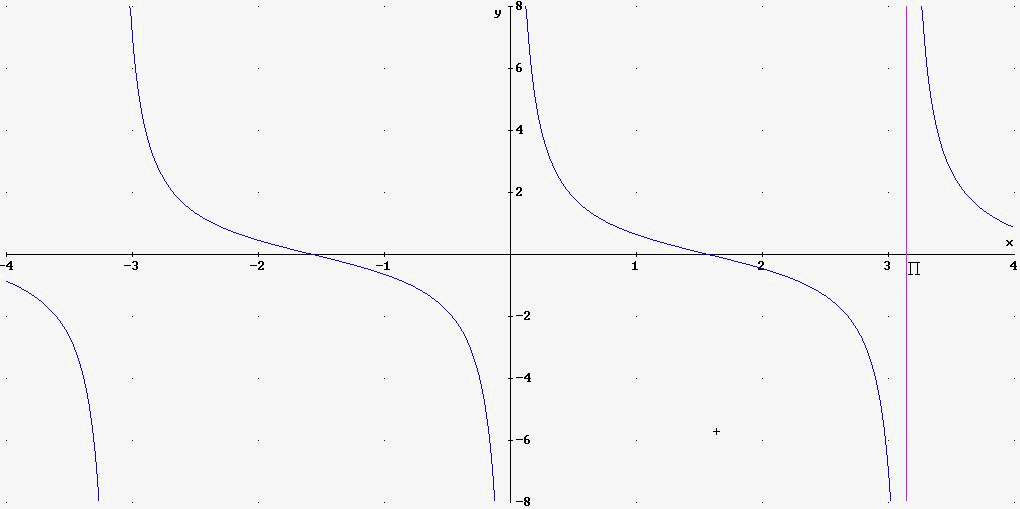
LE FUNZIONI INVERSE DELLE FUNZIONI GONIOMETRICHE
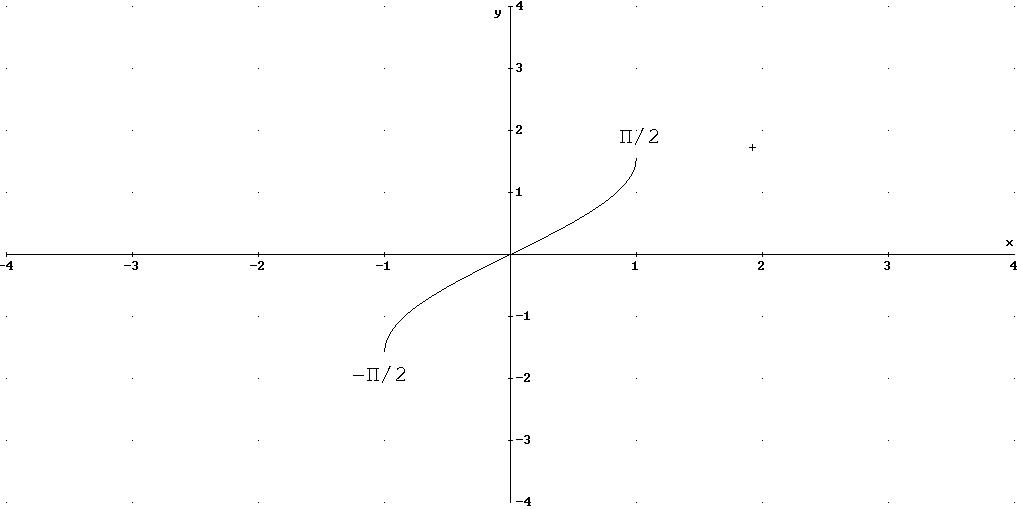
Y=arcsen(x)
y=arccos(x)
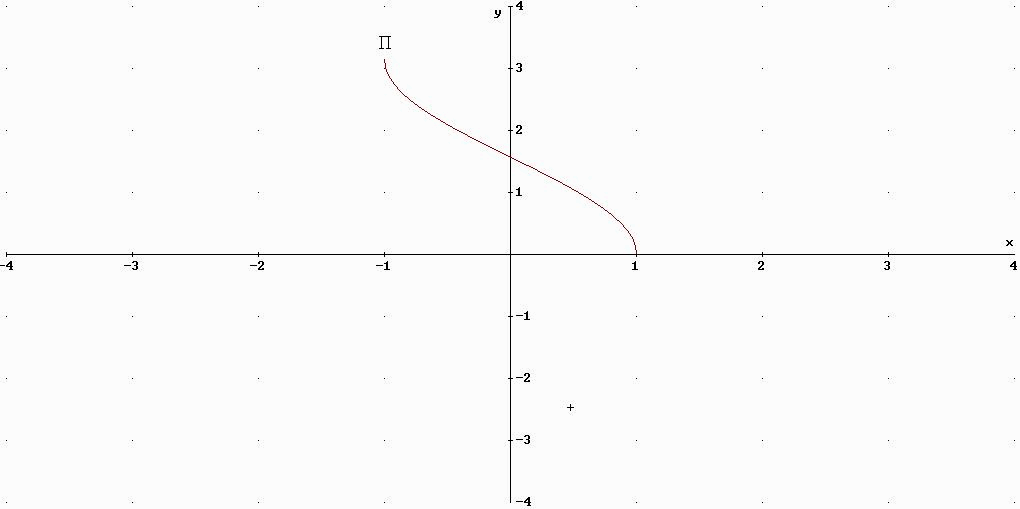
Y=arctg(x)
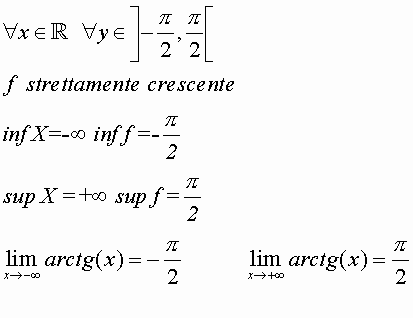
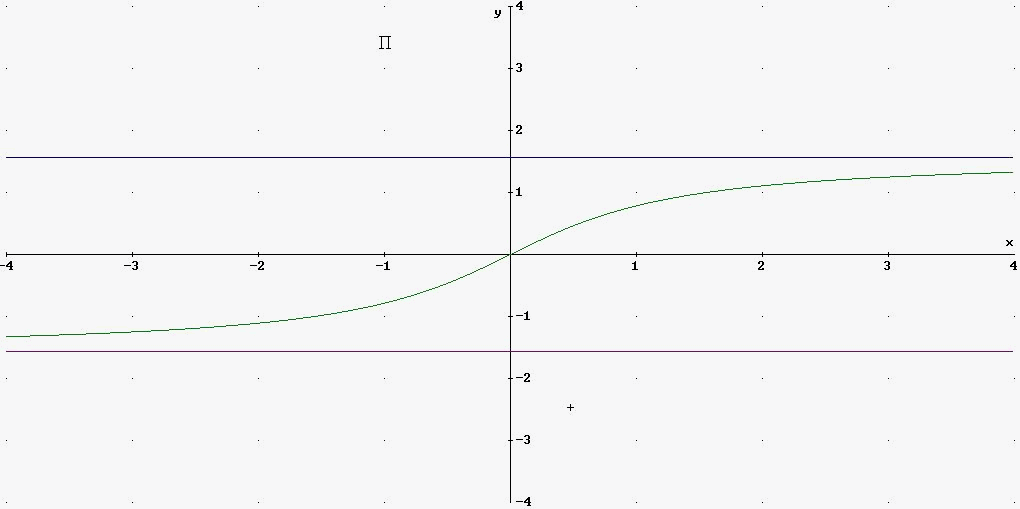
y=arccotg(x)
