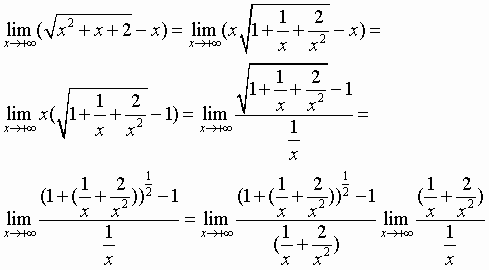![]() Infinitesimi e
infiniti
Infinitesimi e
infiniti
Si dice che la funzione ![]() è un
infinitesimo in
è un
infinitesimo in ![]() quando risulta:
quando risulta:
![]()
![]()
Si dice invece che f è un infinito in
![]() quando risulta:
quando risulta:
![]()
In particolare:
f infinito positivo in
![]()
![]()
![]()
f infinito negativo in![]()
![]()
![]()
Confronto tra infinitesimi e infiniti.
Ordine di un infinito e di un infinitesimo
Siano assegnate due funzioni f(x) e g(x), infinitesime in
![]() . Confrontare i loro infinitesimi
significa studiare il limite in
. Confrontare i loro infinitesimi
significa studiare il limite in![]() del
loro rapporto, ovvero il:
del
loro rapporto, ovvero il:
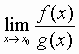 I casi
possibili sono i seguenti:
I casi
possibili sono i seguenti:
1) il limite è uguale a 0. Si dice allora che f è un infinitesimo di ordine superiore rispetto a g
2) il limite è uguale a![]() .Si
dice allora che f è un infinitesimo di ordine inferiore rispetto a g
.Si
dice allora che f è un infinitesimo di ordine inferiore rispetto a g
3) il limite è finito e diverso da 0. Si dice allora che f e g sono infinitesimi dello stesso ordine. In particolare, se l=1 i due infinitesimi si dicono equivalenti
4) il limite non esiste. In tal caso diremo che i due infinitesimi non sono confrontabili.
In modo analogo ragioneremo se le due funzioni sono entrambe infinite in
![]()
In tal caso:
1) il limite è uguale a ![]() . Si
dice allora che f è un infinito di ordine superiore rispetto a g
. Si
dice allora che f è un infinito di ordine superiore rispetto a g
2) il limite è uguale a 0.Si dice allora che f è un infinito di ordine inferiore rispetto a g
3) il limite è finito e diverso da 0. Si dice allora che f e g sono infiniti dello stesso ordine.
4) il limite non esiste. In tal caso diremo che i due infinitesimi non sono confrontabili.
NOTAZIONE DI LANDAU
Se f e g sono infinitesime in ![]() e se risulta:
e se risulta: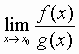 =0 , per esprimere
che f è infinitesimo di ordine superiore rispetto a g si può scrivere:
=0 , per esprimere
che f è infinitesimo di ordine superiore rispetto a g si può scrivere:
![]() (si legge: f o
piccolo g)
(si legge: f o
piccolo g)
La stessa scrittura, riferita a due infiniti, significa che f è infinito di ordine inferiore rispetto a g.
Definiamo ora cosa si intende per ordine di infinitesimo ( di infinito) di una funzione. Per determinarlo occorrerà confrontare la nostra funzione con un’altra, indichiamola con u(x),scelta come infinitesimo ( infinito) campione.
Se risulta: 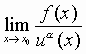 con
con![]() >0
>0
diremo che f(x) è un infinitesimo ( infinito)di ordine
![]() .
.
Può naturalmente accadere che non esista alcun numero reale
![]() tale che f sia infinitesimo in
tale che f sia infinitesimo in![]()
di ordine ![]() . In particolare
diremo che f(x) è un infinitesimo di ordine infinitamente grande quando,
qualunque sia
. In particolare
diremo che f(x) è un infinitesimo di ordine infinitamente grande quando,
qualunque sia ![]() , f è di ordine
maggiore di
, f è di ordine
maggiore di ![]() . Diremo invece che è
un infinitesimo di ordine infinitamente piccolo quando, qualunque sia
. Diremo invece che è
un infinitesimo di ordine infinitamente piccolo quando, qualunque sia
![]() , f è di ordine minore di
, f è di ordine minore di
![]() .
.
Si verifica facilmente che:
Se f è un infinitesimo in ![]() ,
,![]() è un infinito in
è un infinito in ![]() , e viceversa.
, e viceversa.
Se f è di ordine maggiore, uguale o minore di
![]() , anche
, anche
![]() è dello stesso ordine.
è dello stesso ordine.
Nella scelta degli infinitesimi campione, u(x), ci orienteremo così:
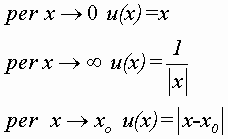
Invece, per gli infiniti campione:
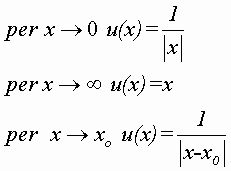
Infinitesimi equivalenti
Abbiamo detto che due infinitesimi sono equivalenti se risulta: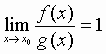
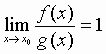
In tal caso scriveremo: f equiv g, ovvero:![]()
Nel caso in cui risulti:
![]()
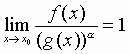
chiameremo parte principale di f rispetto a g il prodotto:
![]()
Evidentemente allora:
![]()
Ad esempio, poiché:
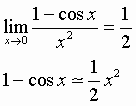
Sono utili allo scopo del calcolo dei limiti le proposizioni seguenti:
1) ![]()
![]()
2) 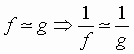
3) 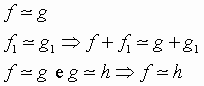
4) Aggiungendo o sottraendo ad un infinitesimo f un infinitesimo di ordine superiore, si ottiene un infinitesimo equivalente ad f.
Aggiungendo o sottraendo ad un infinito f un infinito di ordine inferiore, oppure una funzione limitata, si ottiene un infinito equivalente ad f.
5) 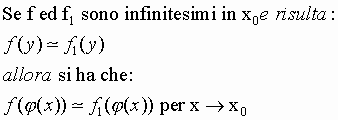
INFINITESIMI ED INFINITI NOTEVOLI
Al tendere di x verso 0(![]() )
, l’infinitesimo ( l’infinito)
)
, l’infinitesimo ( l’infinito)
![]()
Al tendere di x verso 0, gli infinitesimi
![]() , tg x,
arcsen x, arctg x, log(x+1),
, tg x,
arcsen x, arctg x, log(x+1), ![]() ,
,
sono tutti equivalenti all’infinitesimo x e quindi sono tutti di ordine 1
Per 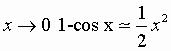 e quindi 1- cos x è
un infinitesimo di ordine 2;
e quindi 1- cos x è
un infinitesimo di ordine 2; ![]() ed è un infinitesimo del primo ordine;
ed è un infinitesimo del primo ordine;
![]() , infinitesimo di ordine 1;
, infinitesimo di ordine 1;
![]() , infinitesimo di ordine 1;
, infinitesimo di ordine 1;![]()
Al tendere di x verso ![]() l’infinitesimo
o infinito
l’infinitesimo
o infinito ![]() è di ordine
infinitamente grande ( e quindi non è dotato di ordine)
è di ordine
infinitamente grande ( e quindi non è dotato di ordine)
Al tendere di x verso 0 ( o verso
![]() ) l’infinito
) l’infinito
![]() è di ordine infinitamente
piccolo
è di ordine infinitamente
piccolo
( quindi non è dotato di ordine)
E’ facile inoltre verificare che:
Siano a e b due numeri reali > 1 e si abbia. a>b. Allora al tendere di x
verso ![]() ( ovvero verso -
( ovvero verso -![]() )
il primo dei due infiniti è di ordine superiore rispetto al secondo;
)
il primo dei due infiniti è di ordine superiore rispetto al secondo;
Qualunque sia ![]() , per x che
tende a 0 l’infinitesimo
, per x che
tende a 0 l’infinitesimo ![]() è di
ordine minore di r , ma maggiore di
è di
ordine minore di r , ma maggiore di
![]() ,
,
![]() , sicché tale infinitesimo
non è dotato di ordine
, sicché tale infinitesimo
non è dotato di ordine
![]() ,
,
![]() l’infinitesimo
l’infinitesimo
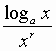 è di ordine minore di r , ma
maggiore di
è di ordine minore di r , ma
maggiore di ![]() ,
,
![]() , sicché tale infinitesimo
non è dotato di ordine;
, sicché tale infinitesimo
non è dotato di ordine;
![]()
![]() l’infinito
l’infinito
![]() è di ordine maggiore di r,
nonché di ordine minore di
è di ordine maggiore di r,
nonché di ordine minore di ![]()
![]() ,
sicché tale infinito non è dotato di ordine;
,
sicché tale infinito non è dotato di ordine;
Siano f e g due infinitesimi in
![]() , oppure infiniti. Se f e g
sono dello stesso ordine, allora
, oppure infiniti. Se f e g
sono dello stesso ordine, allora
![]() sono equivalenti;
sono equivalenti;
Sia f un infinito positivo in
![]() . Se f è dotato di ordine,
allora l’infinito
. Se f è dotato di ordine,
allora l’infinito ![]() è di ordine
infinitamente grande.
è di ordine
infinitamente grande.
ESEMPI ED APPLICAZIONI
Al tendere di x verso 0 si ha che:
![]()
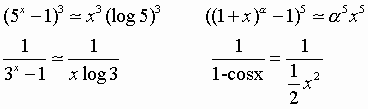
E, in modo analogo:
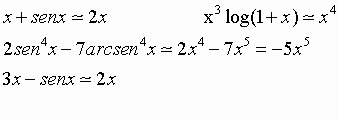
Sono inoltre valide le seguenti uguaglianze:
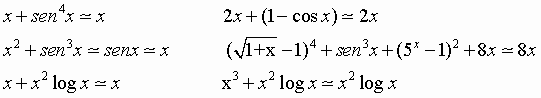
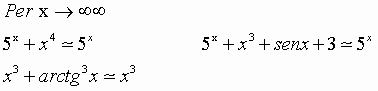
Per le proprietà delle funzioni composte:
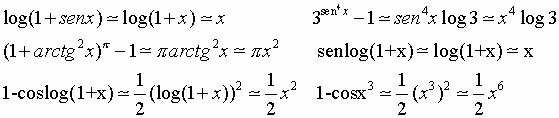
Al tendere di x verso ∞ si ha che:
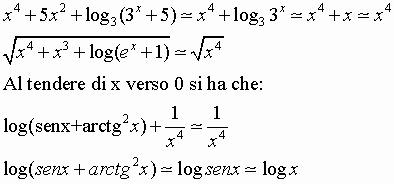
TEOREMI SUI LIMITI CHE SI PRESENTANO
IN FORMA INDETERMINATA
Forme indeterminate 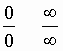
Siano:

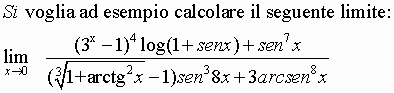
Poiché il numeratore è equivalente a

Il limite proposto è uguale al seguente:
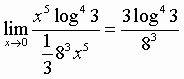
E, analogamente:
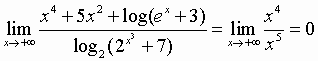
FORMA INDETERMINATA 0*∞
Sussistono le proposizioni seguenti:
1)Siano 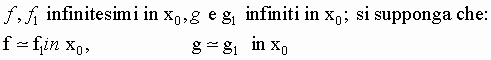
Se esiste uno dei limiti:
![]()
allora esiste anche l’altro e i due limiti sono uguali.
2) Sia f un infinitesimo in![]() e g un infinito in
e g un infinito in ![]() .
.
Se f è di ordine r e g di ordine minore di r,allora risulta:
![]()
relazione che sussiste anche se g è di ordine r e f di ordine maggiore di r.
3) Siano f un infinitesimo in
![]() e
e
![]() un infinitesimo o un infinito in
un infinitesimo o un infinito in
![]() . Se f e
. Se f e
![]() sono dotati di ordine , risulta:
sono dotati di ordine , risulta:
![]()
Si voglia ad esempio calcolare il limite:
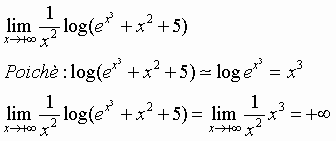
Per la proposizione 3):
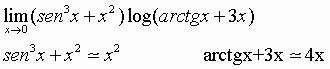
i due infinitesimi a primo membro sono dotati di ordine, sicché il limite proposto è uguale a 0.
FORMA INDETERMINATA +∞-∞
Sussiste la proposizione:
Siano f e g infiniti positivi in
![]() , sicché il limite
, sicché il limite
![]() (*)
(*)
si presenta nella forma indeterminata +∞ -∞
Se in ![]() f è di
ordine superiore rispetto a g, allora il limite esiste ed è +∞.
f è di
ordine superiore rispetto a g, allora il limite esiste ed è +∞.
Se, detto ![]() un
infinito positivo in
un
infinito positivo in ![]() risulta:
risulta:
![]()
con![]() , allora il
limite (*) è uguale a
, allora il
limite (*) è uguale a ![]()
Negli altri casi occorrerà procedere con opportuni artifizi.
Esempio:
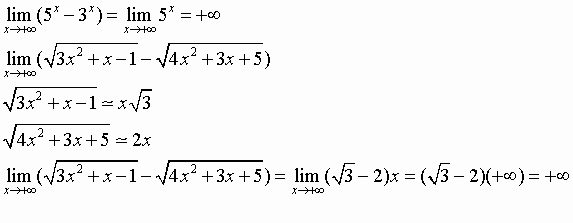
Osserviamo infine il seguente limite, al quale non sono applicabili le precedenti proposizioni:
![]()
Si può procedere razionalizzando. Ma vi è anche un altro elegante procedimento: